DSP Basics

What is DSP ?

Digital Signal Processor device which takes digital signal and alters them through different algorithms and provides the results within milliseconds. These are normally found in Speakers, Mobiles..

In audio applications, DSP plays a key role to use different features like ANC, adaptive filtering, Noise suppression..

Digital Signal Processing :

X(t) -> Anti aliasing -> Sample & hold ->  ADC -> DSP -> DAC -> Reconstructed signal -> Y(t)

Audio Processing - Modification audio within same domain 

Sampling - Converting the continuous signal into discrete signal 

Importance of Sampling in DSP:

• Digital Representation: Enables analog signals to be represented digitally, which is essential for digital storage, processing, and transmission.
• Discrete Processing: Allows the use of digital algorithms and systems that are more robust and flexible compared to their analog counterparts.
• Accuracy and Efficiency: Facilitates precise and efficient manipulation of signals using digital techniques.

Nyquist Theorem - Samples that can be reconstructed back when sampling at frequency higher than                                     the maximum frequency

Nyquist rate - Rate at which a signal can be re-constructed after sampling

                            fs >2fmax

Why Nyquist theorem is critical in DSP?

• Preventing the aliasing 
• Signal reconstruction

ex: For 10khz signal will have to sampled at greater than 20khz 

                            if sampling rate > nyquist rate -> Signal oversampled

                               sampling rate < nyquist rate -> Signal undersampled also know as Aliasing

In the below figure freq = 1000, time = 0.01 sec sampling rate = 48000

No of samples present in this signal = Max-frequency * Time * Sampling frequency

                                                          = 1000 * 0.01 * 48000

                                                          = 480 samples

For one single cycle   = Max-frequency * Time * Sampling Rate 

                                   = 1000 * 0.001 * 48000

                                   = 48 samples

                    

In audacity, we can't generate a tone more than the half of the sampling frequency as shown below 

It will not generate because its not satisfying the nyquist criteria which fs > 2fmax

In the above example I'm using sampling frequency = 48K and max frequency should have be less than 24K

we will not get any waveform if it exactly Fs/2 as shown below

Even if select less than the Fs/2 also sometimes we will not get exact sine wave because theoretically nyquist rate should have to Fs > 2Fmax but practically Fs > 2.5Fmax.

Even if re-sample we will not get proper sine wave because signal already lost which we can't restore

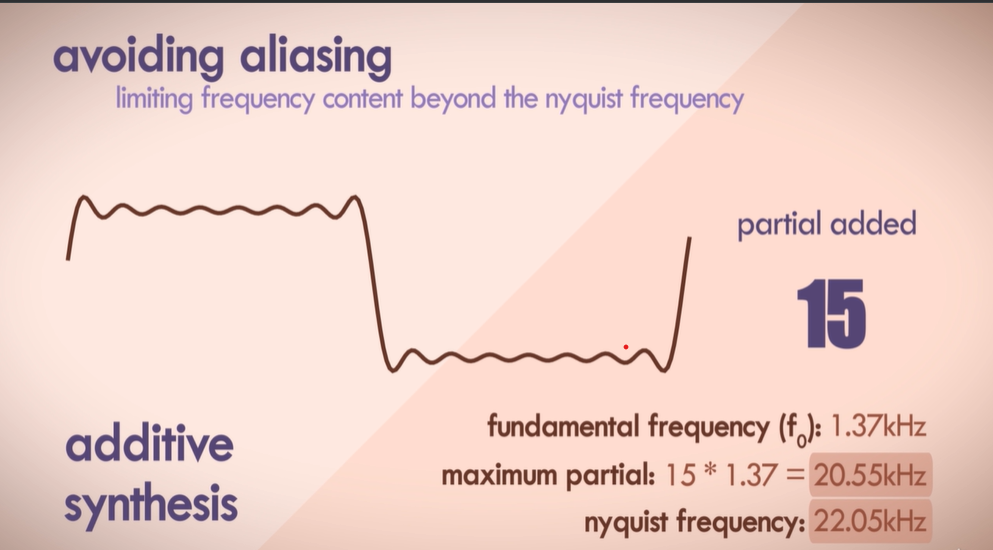
Anti-Aliasing - pre-alias apply low pass filter to attenuate high sampled frequencies  

Interpolation & Decimation:

Quantization - Process of converting discrete time domain signal to discrete time discrete amplitude                              signal

Quantization error - Difference between quantized value & original value 

Bit Rate - No.of bits transferred or processed from one point to another point in one second

Bandwidth - Total amount of data transferred or processed from one point to another point in one second

Bandwidth is capacity and bitrate is transfer rate

Multirate signal processing: 

Interpolation : Process of increasing the sampling rate of a signal. It involves two steps

• Up sampling is done by inserting the L-1 zeros in the original signal, Where L is interpolation factor
• Filtering is to smooth the signal after interpolation & interpolate the zeros in between original signal

Decimation : Process of decreasing the sampling of a signal

• Filtering is done to remove unwanted high frequencies which may cause aliasing
• Down sampling is performed by taking M th sample and discard the rest of samples, where M is the decimation factor

 Digital Filters:

1. IIR Filter - Infinte Impluse Response

2. FIR filter - Finite Impluse Response 

IIR Filters:

Pros:

• Requires less coefficients & memory
• It has low latency, so used for any real time applications in RF

Cons:

• It is not stable compared to FIR 
• Need more analysis while implementing in fixed point especially using Direct FormII which will overflow
• It has non-linear phase 

FIR Filters:

Pros:

• Easier to implement
• More stable than IIR filters
• It has linear phase
• It has better performance

Cons:

• It requires more memory
• It has high latency

 Designing of FIR filter : We can design fir filter in two different ways.

1. Filter coefficient's forward & input backwards

2. Filter coefficient's backward & input forward 

                equation 1: 

                    equation 2: 

Here  x - input

          b - Impulse response

          z - delay 

C Code:

Fir data flow: 

	Index	insamp	input buffer	Coeffcients
Set insamp buffer with 0	0	0	0	0
	1	0	1	1
	2	0	2	2
	3	0	3	3
	4	0	4	4
	5	0	5	5
	6	0	6	6
	7	0	7	7
	8	0	8	8
	9	0	9	9
	10	0	10	10
	11	0	11	11
	12	0	12	12
	13	0	13	13
	14	0	14	14
	15	0	15	15
copy input buffer  to insamp buffer from location 16	16	0
	17	1
	18	2
	19	3
	20	4
	21	5
	22	6
	23	7
	24	8
	25	9
	26	10
	27	11
	28	12
	29	13
	30	14
	31	15

I = 0			I = 1			I = 2			I = 3
in		coeff	in		coeff	in		coeff	in		coeff
0	*	15	0	*	in0	0	*	in1	0	*	in2
1	*	14	1	*	15	1	*	in0	1	*	in1
2	*	13	2	*	14	2	*	15	2	*	in0
3	*	12	3	*	13	3	*	14	3	*	15
4	*	11	4	*	12	4	*	13	4	*	14
5	*	10	5	*	11	5	*	12	5	*	13
6	*	9	6	*	10	6	*	11	6	*	12
7	*	8	7	*	9	7	*	10	7	*	11
8	*	7	8	*	8	8	*	9	8	*	10
9	*	6	9	*	7	9	*	8	9	*	9
10	*	5	10	*	6	10	*	7	10	*	8
11	*	4	11	*	5	11	*	6	11	*	7
12	*	3	12	*	4	12	*	5	12	*	6
13	*	2	13	*	3	13	*	4	13	*	5
14	*	1	14	*	2	14	*	3	14	*	4
15	*	0	15	*	1	15	*	2	15	*	3
			Introduce one delay for each iteration

References:

https://sestevenson.wordpress.com/implementation-of-fir-filtering-in-c-part-1/